The Earl’s Machine

In 2008, I curated the widely-acclaimed exhibition of a very rare calculating machine invented by the extraordinary and colourful Charles, 3rd Earl Stanhope (1753-1816) at the Winter Fine Art & Antiques Fair, Olympia by courtesy of the Trustees of the Chevening Estate. Chevening in Kent was the home of the Stanhope family for almost 250 years before it was placed in trust for the nation on the death of the 7th Earl in 1959. The current occupant of Chevening is the Foreign Secretary. It was believed that this is the first time that the calculator has left the house since the 3rd Earl’s death in 1816.
Made and cased by James Bullock in c 1777, Earl Stanhope’s “arithmetical machine” solved problems in multiplication and division by the revolution of a small winch. It was the world’s first calculating machine to tackle the tens carry mechanism and is a marvel of 18th century ingenuity. One of only three surviving examples, the machine is seen today as a forerunner to the modern computer age.
Here is my text for the exhibition catalogue together with a fascinating piece by Michael Wright M.A., M.Sc., F.S.A, a mechanician and historian of mechanism, on the working of the calculating machine.
‘Citizen Stanhope’
By any reckoning Charles Stanhope, third Earl Stanhope, was a remarkable man who led a life of extraordinary contradiction. Born to aristocratic privilege, he devoted his life to radical causes. He called himself ‘Citizen’ Stanhope yet enjoyed the benefits of his estate at Chevening. He opposed war with France but proposed means of waging it. He posed as a puritan but supported non-conformism. He avowed liberty but terrorised his own family. His name is obscure yet elements of his work are still in use today.
But Stanhope’s achievements were real, and lasting, and they provide the final irony to the earl’s complicated life when today he is known, if at all, principally as the draconian father of the celebrated adventuress Lady Hester Stanhope. Moreover the causes he espoused, often in much-vilified isolation, resonate as loudly today as they did in his lifetime; while the arguments he pursued in favour of liberty continue to provoke public interest and unsettle government.
The physical relics of his life provide the most vivid path into the earl’s obsessions. As his wonderful calculating machine testifies, Stanhope was far more than an amateur dabbler in the technological developments of the eighteenth century. He brought to the emerging mechanical age a boldness of vision, an elegance of execution and a sense of artistry unrivalled until Charles Babbage’s experiments in the 1830’s.
In fact, almost the only conventional thing about Stanhope was his birth, on 3 August 1753. His father, the second earl, was himself a highly cultivated man although an interest in mathematics and the sciences had been suppressed by his kinsman, the eminent classicist and man of letters Lord Chesterfield. As second son Charles was not expected to succeed to his father’s title and estates. However, when his elder brother Philip died of consumption in 1763, Charles replaced him as heir, assumed the courtesy title Viscount Mahon and, as the Stanhopes’ sole surviving son, became the focus of their ambition and anxious concern. Fearing he might suffer the fate of his brother, Charles was removed from Eton to join his parents in the more wholesome air of Switzerland. The following decade spent in Geneva came to define Charles’s political outlook and sharpened his fascination for social progress and technological innovation.
Although the second earl steadfastly refused to pay court to the radical philosopher Voltaire, then resident in Switzerland, his son was intoxicated by the free thinking political arguments swirling around Geneva’s ancient streets developing a deep-seated admiration for the civic model established by the city’s rulers. He adopted the Genevese simple manner of dress—later the cause of much comment in London—and came to share their distrust of the theatre and, indeed, of frivolity generally. Yet Charles was not entirely devoted to study, or to serious pursuits. An accomplished painter, he joined a society of artists training under the eye of Jean-Étienne Liotard. He was also an enthusiastic archer becoming commander of the prestigious Ancient Order of Archers and Dragoons and thence to a coveted place on Geneva’s legislature, known as the Council of Two Hundred.
Charles’s interest in politics continued after the Stanhopes returned to England in 1774. Shirking the riotous and decadent behaviour of so many of his aristocratic peers, he concentrated on entering parliament. An early attempt proved unsuccessful but his marriage, in December 1774, to Hester Pitt—the daughter of one Prime Minister and sister of a future one—transformed his political prospects. Charles finally entered the commons in 1780 and a successful career in government seemed assured. Yet his radical instincts, nurtured in Geneva, soon brought him into conflict with the political elite and, eventually, with his brother in law William Pitt the Younger. A known associate of establishment bête-noir John Wilkes, Charles vociferously agitated for electoral and financial reform whilst championing the rights of religious dissenters and Catholics. Many in government were relieved when Charles succession as third Earl Stanhope in 1786 caused his removal from the Commons. Almost immediately, however, he resumed his campaigns in the House of Lords concentrating, for a time, on the need for religious tolerance.
Stanhope was equally energetic away from Westminster. A childhood fascination with mechanics and mathematics was soon put into practice. Elected to the Royal Society at twenty, Stanhope embarked on a series of self-funded experiments. These always had a social function in mind such as improving the burning of lime for mortar used in the building trade, or developing more sophisticated roofing materials. One of his most dramatic demonstrations, encouraged by a friendship with the gas engineer Joseph Priestley, followed a lengthy investigation into fireproofing houses by starving the fire of air. A group of friends and celebrities were invited to eat ice creams in a purpose built wooden folly at Chevening while a fire raged beneath them. His installation of fire doors at Chevening saved the house from total destruction following a fire in 1797. Another famed acquaintance, Benjamin Franklin, led to Stanhope’s study of electricity and his publication in 1778 of ‘Principles of Electricity’, a highly-regarded treatise on the new science.
It was in this challenging and high achieving intellectual climate that Stanhope designed and built his calculators, or ‘arithmetical machines’, between 1775 and 1780. The machines typify his obsession with technical innovation whilst retaining a practical, rather than theoretical application. Indeed, the earl never sought financial reward for any of his inventions—which over time badly drained his fortune—preferring to see them, like his politics, as the practical means to a more enlightened age.
Stanhope’s private life was as rewarding as his experiments during the 1770’s. By all accounts he was a devoted husband and an indulgent father to his daughters: the tomboyish Hester and bookish Griselda. However, the decade ended in tragedy when Stanhope’s wife Lady Hester died, aged just twenty five, of complications following the birth of a third daughter, Lucy. Although he married again quickly—his second wife Louisa Grenville was a cousin of his first—it was not a love match and despite four more children, this time all sons, the marriage drifted into estrangement.
The deaths of his beloved Hester and then of his father seem to have further hardened Stanhope’s attitude towards his own class and the political system which sustained it. His eccentricity of dress and speech became more pronounced, and his outlook still more dogmatic and unyielding. In the eyes of many, these traits assumed a sinister edge amid the political turmoil caused by the defining event of Stanhope’s life: the French Revolution.
As chairman of the Revolution Society, founded to perpetuate the memory of the England’s own Glorious Revolution in 1688, Stanhope responded with gusto to the unfolding drama in Paris. He dispatched a letter of congratulation to the French National Assembly and, in the heady days before the Terror, sustained an enthusiastic correspondence with the Marquis of Condorcet, later published in France to propaganda effect. In a further gesture of fraternal solidarity, the earl removed the coronets from the gateposts at Chevening (long since restored) and removed from display a magnificent tapestry given to the first earl by the King of Prussia.
Stanhope’s possible role as intermediary was seized upon by both sides as war between France and England seemed inevitable following the fall of the French Monarchy in 1792. He was simultaneously pressed by the English to negotiate the freedom of the royal family while the French diplomat Prince Talleyrand sought the earl’s intervention to preserve the peace. When war came, in February 1793, Stanhope declared it the most important, and heartbreaking, occasion in his life. In a series of bitter and impassioned speeches he accused the British government of treachery. ‘You will not make this a war of the people of Great Britain’ he raged, ‘it is a war of the Government of England against the funds of England, against her paper currency, against her best and dearest interests.’ Defiantly, the earl, now self-styled ‘Citizen Stanhope’, continued to correspond with the enemy declaring in parliament that ‘I am ready to be hanged or guillotined for the cause of liberty. It is not what I wish or call for, but I hope if it became necessary I should not shrink from it.’ But with his country at war, even the earl’s political friends found his stance hard to defend while it caused a permanent breach with his brother-in-law William Pitt. To celebrate Stanhope’s isolation, a medal was struck to honour ‘The Minority of One’ but in 1795 the earl withdrew from parliament on a matter of principle, proudly asserting that ‘I have put my foot on the rock of liberty and justice, and from the rock I never will depart.’
Stanhope faced constant harassment during his secession from parliament: from the press, the public and a suspicious government; but he was not idle. He returned to his inventions, converting the fine drawing room at Chevening into a busy workshop. His fertile imagination had turned to steam engineering. After consulting Matthew Boulton and James Watt, the leaders in the field, the earl designed and built a series of steam boats culminating in Kent, an ‘Ambinavigator’ or double bowed, cigar shaped vessel propelled by a single steam driven paddle or ‘vibrator’. At vast personal expense the earl submitted Kent to sea trials and despite his deep opposition to the war, offered her to the Admiralty. But the difficulties of maintaining steam propulsion at sea proved insuperable and in 1798 Kent was scrapped, losing the earl a further fortune. Undaunted, Stanhope worked on better means of ship construction, for years bombarding the Admiralty with his suggestions on how to stem the terrible attrition rate in the Royal Navy. He also engaged the American engineer Robert Fulton to help him devise methods of cutting canals through his undulating West Country estate at Holsworthy. Their ambitious plans came to nothing and within a few years Fulton—who returned to America to offer his engineering services to France—and Stanhope were pitched against each other when the earl devised a method for defending ships against Fulton’s proto-torpedoes.
Stanhope’s most significant contribution was to the printing industry. Alongside the ‘Stanhope Press’—a sophisticated iron hand-press with a novel lever and screw mechanism which was used to print The Times until the arrival of steam presses—the earl developed a system of logotypes and perfected a means of stereotyping adopted by both Oxford and Cambridge University Presses. Characteristically, Stanhope was driven in these projects by a desire to propagate learning through cheaper schoolbooks though they, yet again, placed a severe burden on his own finances. They also exacted a heavy price on his private life.
By 1800, two of the earl’s daughters Griselda and Hester had sought refuge from their obsessional father by moving to the household of their bachelor uncle William Pitt. The third, Lucy, had already eloped with the family doctor. Stanhope’s sons by his second marriage fared little better. The eldest, Philip, fled Chevening to live abroad while his brothers hastily entered the army and navy to their father’s fury. In retaliation for the mass desertion of his family, Stanhope disinherited all his children leaving the bulk of his estate to his mistress, a Mrs Walburgh Lackner, who had originally been engaged as the children’s music teacher. Stanhope’s financial tussles with his family led, to the delight of the press, to his being successfully sued by his own heir. His humiliation in court haunted the earl for the rest of his life.
Stanhope’s political activity revived in the new century. Although he still sought peace with France, his views were tempered by a deep hostility towards Bonaparte who he accused of hijacking the revolution for personal self-aggrandisement. He returned to parliament and resumed his probing of the government predominately on issues surrounding the national currency, a subject in which he had always taken a keen interest. With typical energy, he also led the parliamentary campaign against the slave trade, unwittingly joining a populist movement for the first time in his career. With the passing of the abolition bill in 1807, Stanhope took up the cause of the oppressed closer to home by championing the rights of prisoners and agitating for judicial reform.
Stanhope’s final years were spent in increasing seclusion at Chevening. A longstanding interest in the principles of logic led to a long treatise on the subject and the manufacture of a ‘Logic Demonstrator’ for practical display. He also perfected the ‘Stanhope Lens’, a powerful pocket microscope with broad popular appeal. Sadly, he was less interested in his own well-being living on a diet of soup and barley water and allowing Chevening to fall into disrepair around him. He died, some thought of starvation, on 17 December 1816. A week later, according to the earl’s express wishes, he was interred ‘as a very poor man’ in the family vault at Chevening church, his body being carried there from his house nearby.
In death, Stanhope was accorded the regard he had so lacked in life. The political struggles of the 1780’s were a distant memory and his obituarists warmly praised his lack of pretension and spirited independence. But their eulogies were not without qualification. The earl’s executor Lord Holland considered his late friend ‘an ingenious, diligent, disinterested, useful and remarkable man’; but he could not deny that ‘in his private character he was less praiseworthy’ judging him ‘a bad husband [and] an unkind, perhaps an unjust, father.’ Yet no one faulted the earl’s fanatical dedication to science and the arts, or his skills as a mechanic. Although abrasive in political debate, Stanhope was entirely self-effacing about his inventions. Alongside such ardent self-promoters as Matthew Boulton and Charles Babbage, his contribution to the progress of science is easily dismissed as that of an eccentric dilettante, and his reputation has suffered as such. But, as Michael Wright explains, Charles Babbage, the pioneer of modern computing who owned the earl’s only other surviving calculator (now in the Science Museum), appears to have adopted elements of Stanhope’s engineering in his own groundbreaking work. It is to be hoped, therefore, that the emergence from Chevening of a second machine, in perfect running order despite the passage of 230 years, will enhance the earl’s standing in the scientific world and promote wider interest in an underrated genius.
Martyn Downer, November 2008.
‘The Earl’s Machine’
Crunching Numbers by Mechanical Arithmetic
Perhaps it was at the University of Geneva, where he went to study on leaving Eton, that the young Charles Stanhope, Viscount Mahon, first thought of building a calculating machine. There he studied mathematics under Georges-Louis Le Sage, an inventive man with whom he conducted an extensive correspondence. Through him, Stanhope might have heard of earlier attempts to develop such a device.
The first calculator to become widely known was the Pascaline, devised in 1642 by Blaise Pascal who actually attempted its manufacture for sale. In 1673 Sir Samuel Morland published a book advertising machines that he had devised in 1666. Delivering himself of the statement “It is unworthy of excellent men to lose hours like slaves in the labour of calculation which could safely be relegated to anyone else if machines were used”, the great Gottfried Wilhelm von Leibniz devised his “Stepped Reckoner” in the 1670s. Other machines, and schemes for machines, followed during the eighteenth century. From the later 1770s Phillip Matthäus Hahn built machines on Leibniz’s principle; but Stanhope’s 1777 machine is quite different from earlier machines in nearly every respect, and seems an original invention.
Some machines were suitable only for addition and subtraction. While any adding machine can perform multiplication and division by adding or subtracting repeatedly, machines like Pascal’s – in which numbers were entered digit by digit using a stylus – were not convenient for such repetition. In Leibniz’s machine the numbers were set first, and then the turn of a hand-winch, to execute the addition, might easily be repeated; but even then the “carrying of tens” was not wholly automatic. Furthermore, none of these machines was really reliable.
Whatever his inspiration, Stanhope worked on several different designs. A later machine by him, dated 1780, echoes the simplicity of Morland’s, but the 1777 machine for multiplication and division rivals, and surpasses, Leibniz’s.
The idea is simple. In multiplication, a number (the multiplicand) is added a certain number of times (the multiplier) to generate a product. In division, a number (the divisor) is subtracted from the dividend as many times as possible; the latter number is the quotient, and any part of the dividend that is left, smaller than the divisor, is the remainder. Essentially, each operation is the reverse of the other; so a machine that can perform one can, in principle, be reversed to perform the other.
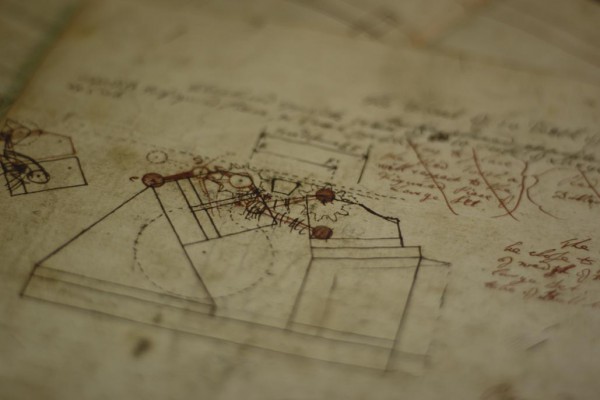
The numbers for the calculation are represented by rows of wheels and rings, each bearing the figures 0 to 9, rotated beneath three slots on the top of the machine through which one figure on each is read. Below the middle slot, and turned directly by the winch, is a drum of figure-rings. The operator begins by moving these round individually to set the multiplicand (or divisor), using the ivory-handled stylus. Besides the figures, each ring bears nine teeth. At the end of the drum is a wheel with cam plates on its faces, acting between fixed guides. As the drum is turned the cams force it to slide axially – from left to right and then back – at definite points in its revolution, which throws the teeth on the rings into and out of gear with a row of ten-toothed gears attached to figure-wheels in a counting array behind. The initial setting of a figure-ring, to show a particular number, turns it round on the drum so that at each turn of the winch only that many of its nine teeth drive the ten-tooth gear before the cam action disengages them. Thus the corresponding figure-wheel of the counter is moved by just that many spaces, and the number is added to (or subtracted from) the display at the back. When multiplying, the display is initially set to zero and the multiplicand on the drum is repeatedly added to it to form the product. When dividing, the back display is initially set to show the dividend, and the divisor on the drum is repeatedly taken away.
Another row of figure-wheels, at the front, records the number of revolutions of the drum: the multiplier (or quotient). During multiplication this number is reduced by one at each turn of the drum, so it is initially set to show the multiplier and drum is turned until the number falls to zero. In division, each turn of the drum adds one to the quotient, until the dividend is reduced to a remainder. An ivory label on the end of the case, bearing arrows marked M (for multiplication) and D (for division), indicates which way the winch must be turned.
Mechanical subtleties make the operation faster and more certain. The most important is the arrangement for “carrying tens”. As children we learned that when the sum of two numbers exceeds nine, “ten is carried” to the next place to the left; and when a greater number is subtracted from a lesser, “ten is borrowed”. Stanhope’s machine is the first in which this “carrying” operation was wholly automatic. Whenever one of the figure-wheels at the back is moved from 9 to 0 in addition (or from 0 to 9 in subtraction), a pin projecting from it trips a corresponding spring-loaded tumbler. Below the figure-wheels and tumblers is a shaft. As the cycle continues, teeth on the cam wheel engage a gear on this shaft so that it makes one full revolution; arms on the shaft sweep round and reset any tumblers that have been tripped, and in doing so move the next figure-wheel to the left by one place. The arms on the shaft are set in a helical pattern, so that these carrying operations take place one after another from right to left, allowing for the possibility that one carrying will lead to another in the next place up. Two sets of arms are fitted, spiralling in opposite directions, and two sets of teeth on the cam wheel make the shaft rotate at two different times during the rotation of the drum. These duplications ensure that the carrying operation is fully performed, whether the machine is rotating forward for multiplication or backward for division.
By copying the process of long multiplication Stanhope reduces greatly the number of times that the winch must be turned. On paper, we multiply separately by the units-figure of the multiplier, the tens-figure, the hundreds-figure … one after the other. In the machine, the drum is shifted along its arbor and each shift to the left corresponds to a move from units to tens, to hundreds, and so on. When a multiplier of several digits has been set in the front array, one of these digits is first reduced to zero. The drum is then shifted and the next digit is reduced to zero, and so on until the whole front array reads zero. As on paper, this may done in any order. The partial calculations are automatically summed in the back array to give the product.
Similarly, the machine mimics the process of long division. The drum is moved to the furthest left position that will still allow the divisor figure to be taken from the dividend in the back counting array. When this has been done as many times as possible, the first digit of the quotient shows in the front array. The drum is then moved one place to the right and the operation is repeated to find the next digit of the quotient, and so on until no more may be taken from the back array, when the number shown there is the remainder.
Rotating the drum moves only one of the front figure-wheels, the one then corresponding to the drum’s selected position; so the front array needs no carry mechanism. The multiplier is reduced to zero, or the quotient is built up, digit by digit, and at each step the drum is never turned more than nine times.
In division, nothing prevents the operator from turning the winch too many times (in effect, making the number in the back array negative). If this happens an ivory ball rises through a hole in the top plate; the operator then turns the winch back, the previous numbers are restored to the displays, and the ball disappears. The same mechanism comes into play in multiplication if the product exceeds the capacity of the array (999,999,999).
We do not know how many of these machines were made. The Science Museum owns one, very similar to the Chevening machine, similarly signed and also dated 1777; so they were made at around the same time and by the same hands, but they are not identical. The Museum’s seems earlier, and may even be a prototype, while the use of a cast brass base plate in the Chevening machine hints at thoughts of a “production run”. The Museum has also a fragment, a small assembly of pieces cut from a third machine. It differs in detail from both complete machines and seems to indicate that further development took place.
We may imagine two great objections to the machine’s widespread use. Firstly, it could clearly never have been reliable. The central figure drum is heavy and robust, but the arrays of counters in front of and behind it, and especially the tumblers for the carry mechanism, are delicate and easily damaged. Secondly, these machines were made by a skilled clock-maker; in 1777 the idea of making machine-parts in quantity to controlled dimensions, so they might be assembled without costly traditional hand-fitting, was still a dream in the minds of only a few men. There were to be generations of development, backed by substantial financial investment (thanks firstly to a military demand for “interchangeable” parts for guns, and later to the public’s voracious appetite for goods such as sewing machines and bicycles), before mechanical products could be made cheaply and yet reliably, according to the “American system of manufactures” that heralded the dawn of Ford’s mass production.
Both the Science Museum’s specimens belonged to Charles Babbage, the pioneer of mechanical computing who first thought of a difference engine – an elaborate adding machine for generating values of mathematical functions – in about 1821, and an analytical engine – a programmable multi-functional machine analogous to a modern electronic computer – in about 1834. It is interesting to notice that the Stanhope machine includes precedents for features of Babbage’s designs, most notably the “successive carry” mechanism.
While Babbage’s grand designs were infamously abortive, Stanhope had foreseen a need that was finally met by more modest machines. First came the Arithmometer, invented by Charles Xavier Thomas de Colmar in 1820; but it was not until the 1870s that, largely redesigned, it became a commercial success. Its final acceptance probably had much to do with other changes that had occurred in those fifty years: the development of new methods of manufacture, and a changed perception of the value of a clerk’s time. It remained in production until the First World War. The most successful mechanical calculator of all time was, however, that invented by Willgodt T. Odhner in 1874. Odhner’s machine bore an astonishing similarity to Stanhope’s both in principle and in layout, except for his crucial invention of “pin-wheels”: wheels with retractable teeth instead of the Stanhope’s figure-rings with fixed teeth, avoiding the need for the destructive cam-action by which Stanhope threw those fixed teeth out of gear. The Odhner machine, its copies and its derivatives, including models that were driven much faster by electric motors, held the field until the widespread introduction of electronic calculators in the 1960s.
Michael Wright M.A., M.Sc., F.S.A.Mechanician & Historian of Mechanism
Honorary Research Associate, Centre for the History of Science, Technology & Medicine, Imperial College, London.